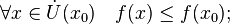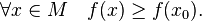Пусть дана функция 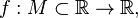 и
и  — внутренняя точка области определения
— внутренняя точка области определения  Тогда
Тогда
 называется точкой локального максимума функции
называется точкой локального максимума функции 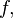 если существует проколотая окрестность
если существует проколотая окрестность 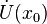 такая, что
такая, что называется точкой локального минимума функции
называется точкой локального минимума функции 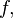 если существует проколотая окрестность
если существует проколотая окрестность 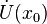 такая, что
такая, что
Если неравенства выше строгие, то  называется точкой строгого локального максимума или минимума соответственно.
называется точкой строгого локального максимума или минимума соответственно.
 называется точкой абсолютного (глобального) максимума, если
называется точкой абсолютного (глобального) максимума, если называется точкой абсолютного минимума, если
называется точкой абсолютного минимума, если
Значение функции  называют (строгим) (локальным) максимумом или минимумом в зависимости от ситуации. Точки, являющиеся точками (локального) максимума или минимума, называются точками (локального) экстремума.
называют (строгим) (локальным) максимумом или минимумом в зависимости от ситуации. Точки, являющиеся точками (локального) максимума или минимума, называются точками (локального) экстремума.
Замечание
Функция 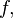 определённая на множестве
определённая на множестве  может не иметь на нём ни одного локального или абсолютного экстремума. Например,
может не иметь на нём ни одного локального или абсолютного экстремума. Например, 
Необходимые условия существования локальных экстремумов
- Из леммы Ферма вытекает следующее:
- Пусть точка
 является точкой экстремума функции
является точкой экстремума функции  , определенной в некоторой окрестности точки
, определенной в некоторой окрестности точки  .
. - Тогда либо производная
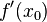 не существует, либо
не существует, либо 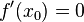 .
.
(Математический Анализ. Том 1. Л. Д. Кудрявцев. Москва «Высшая Школа» 1973 г.)
Достаточные условия существования локальных экстремумов
- Пусть функция
 непрерывна в
непрерывна в 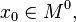 и существуют конечные или бесконечные односторонние производные
и существуют конечные или бесконечные односторонние производные  . Тогда при условии
. Тогда при условии
 является точкой строгого локального максимума. А если
является точкой строгого локального максимума. А если
то  является точкой строгого локального минимума.
является точкой строгого локального минимума.
Заметим, что при этом функция не дифференцируема в точке  .
.
- Пусть функция
 непрерывна и дважды дифференцируема в точке
непрерывна и дважды дифференцируема в точке  . Тогда при условии
. Тогда при условии
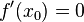 и
и 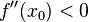
 является точкой локального максимума. А если
является точкой локального максимума. А если
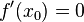 и
и 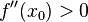
то  является точкой локального минимума.
является точкой локального минимума.
- Пусть функция
 дифференцируема
дифференцируема  раз в точке
раз в точке  и
и 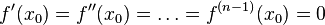 , а
, а 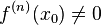 .
.
Если  чётно и
чётно и 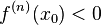 , то
, то  — точка локального максимума. Если
— точка локального максимума. Если  чётно и
чётно и  , то
, то  — точка локального минимума. Если
— точка локального минимума. Если  нечётно, то экстремума нет.
нечётно, то экстремума нет.