Large Scale Numerical Simulation Project

Analysis of solitons in protoplanetary disc with MVS-1000M
Participants:
V. A. Vshivkov (supervisor),
G. G. Lazareva,
V. D. Korneev,
A. V. Snyntnikov,
S. E. Kireev
Abstract:
With MVS-1000M the distribution of particle and gas density in the soliton
were investigated, as well as their velocities, angular momentum, flow
of gas and particles through soliton and vorticity of particle velocity.
It is shown that in the soliton the high values of gas and dust densities
and gas pressure arise. This fact probably explains the synthesis of organic
compounds in protoplanetary disc.
Introduction:
In recent times there is a great interest to the problem of organic matter
genesis in the solar System. In \cite{Gleaves} the protoplanetary disc
is considered as a catalytic chemical reactor for synthesis of primary
organic compounds. The mean density and temperature in protoplanetary
disc are very small. Because of this reason it is extremely important
to find out how do the high values of temperature, pressure and density
appear, that are necessary for chemical synthesis. The solitons that appeared
in our computational experiments present one of the possible answers to
this question.
Source equations
The dynamics of the dust component of protoplanetary disc is described
by the Vlasov-Liouville kinetic equation. In the following text dust particles
will be called simply particles. To consider motion of the gas component
the equations of gas dynamics are employed. The gravitational field is
determined by Poisson equation. If we employ the collisionless approximation
of the mean self-consistent field, then Vlasov-Liouville kinetic equation
is written in the following form:
![]()
where ![]() is
is the time-dependent one-particle distribution function along coordinates
and velocities,
is
is the time-dependent one-particle distribution function along coordinates
and velocities,![]() is the acceleration of unit mass particle,
is the acceleration of unit mass particle, ![]() is
the friction force between gas and dust components of the medium. Gravitational
potential,
is
the friction force between gas and dust components of the medium. Gravitational
potential,![]() , could
be divided
, could
be divided
into two parts:
![]()
where ![]() 1
presents either the potential of immobile central mass (either galactic
black hole or protostar) or the potential of a rigid system which is out
of disc plane (either the stars of galactic halo or molecular cloud).
The second part of potential
1
presents either the potential of immobile central mass (either galactic
black hole or protostar) or the potential of a rigid system which is out
of disc plane (either the stars of galactic halo or molecular cloud).
The second part of potential ![]() 2
is determined by the additive distribution of the moving particles and
gas.
2
is determined by the additive distribution of the moving particles and
gas. ![]() 2 satisfies
the Poisson equation:
2 satisfies
the Poisson equation:
![]()
In the case of infinitesimally thin disc the bulk density
of the mobile media ![]() is equal to zero
is equal to zero ![]() (
(![]() part
is the particle density,
part
is the particle density, ![]() is
the gas density). At the disc with the surface density
is
the gas density). At the disc with the surface density ![]() .This
shear gives a boundary condition for the normal derivative of potential
.This
shear gives a boundary condition for the normal derivative of potential
![]() 2:
2:
![]()
The equations of gas dynamics take the following form:
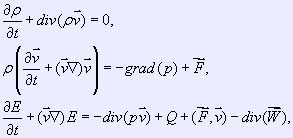
where 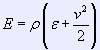 is
the density of gas full energy,
is
the density of gas full energy, ![]() is
the internal energy, p = p(
is
the internal energy, p = p(![]() ,T)
is the gas pressure, W is the heat flow, is the increase of energy
due to chemical reactions and radiation. F is the external force which
is defined by the following expression:
,T)
is the gas pressure, W is the heat flow, is the increase of energy
due to chemical reactions and radiation. F is the external force which
is defined by the following expression:
![]()
where kfr is the coefficient of friction between
gas and dust components of the disc, u is the dust velocity, v is the
gas velocity.
In the case of the flat disc (so called 3D2V model) the form of equation
remains the same with the only exclusion: bulk density ![]() is
replaced with surface density
is
replaced with surface density ![]() .In
this paper, we shall consider only the flat disc model.
.In
this paper, we shall consider only the flat disc model.
In the full description of the protoplanetary disc these equations are
complemented with the equations for chemical reactions in gas phase and
the equations for simulation of coagulation processes in the dust component.
The following quantities were chosen as basic characteristic parameters
for transition to sizeless variables:
– distance from the Sun to the Earth R0=
1.5* 1011m;
– mass of the Sun M0= 2* 1030kg;
– gravitational constant G= 6.67* 10-11m2*
kg-2.
Corresponding characteristic values of the particle velocity V0,
time t0, potential ![]() 0,
density
0,
density ![]() 0(
0(![]() 0)
and pressure p0 are written as:
0)
and pressure p0 are written as:
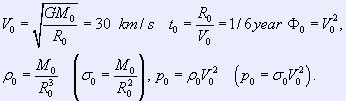
In the following text all the parameters are given in
sizeless units.
Vlasov-Liouville equation is solved by Particles-in-Cells method [2].
To solve the equations of gas dynamics Fluids-in-Cells method is employed
[3].
In the authors' opinion, an efficient Poisson equation solver could be
built only if the peculiarities of the problem were taken into account.
These peculiarities are the following. First, the problem is non-stationary.
Second, at initial moment of time the disc has axial symmetry. And third,
all the matter is situated in the disc plain. Having considered all these
peculiarities, a special Poisson equation solver was built on the basis
of fast Fourier transform [4].
The implemented methods for solution of Vlasov equation and gas dynamics
equations are described in more detail in [5]. Parallelisation scheme
is presented in [6].
Initial distribution of the particle and gas density is set according
to the model of solid body rotation:
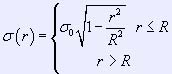
Here R is the radius of the corresponding disc. Initially for radial component of the particles' velocities a normal distribution is set:
![]()
here TD is the dynamic temperature
of particles. An additional parameter is the pressure of gas in the disc
centre.
Parameters of computational experiments:
The technical parameters of computational experiments are given in the
table 1
| Number of grid nodes | NR |
120 |
200 |
300 |
| NR |
128 |
256 |
256 |
|
| Nz |
128 |
128 |
128 |
|
| Number of particles (in millions) |
10 |
20 |
50 |
|
| Computation time (in hours) |
8 |
30 |
49 |
|
| Number of processors |
8.0 |
|||
| Radius of domain |
9.0
|
|||
| Height of domain |
8.0
|
|||
|
Table 1. Technical parameters.
|
||||
The physical parameters that are set as initial data for the computational experiment are given in the table 2. The most important among them are the masses: mass of central body, mass of gas component and mass of dust component
| Radius of dust disc, RP | 1.0 |
| Radius of gas disc, RG | 1.0 |
| Mass of dust component, MP | 1.0 |
| Mass of gas component, MG | 1.0 |
| Mass of central body, M0 | 0.5 |
| Dynamic temperature of dust particles, TD | 1.0 |
| Coefficient of friction, kfr | 1.0 |
| Gas pressure in the centre, p0 | 0.01 |
|
Table 2. Physical
parameters |
|
In the course of computational experiments it was found out that the
solitons definitely arise when the mass ratio is MP : MG
: M0 = 2 : 2 : 1. Also soliton formation is affected by the
coefficient of friction between dust and gas components. When this coefficient
substantionally decreases the solitons do not arise. The increase of the
radius of either gas or dust component affects the system like the decrease
of the corresponding mass and makes the disc more unstable. The dynamic
temperature of dust particles and gas pressure in the disc centre make
the corresponding component of the disc more stable. Nevertheless the
influence of these quantities on the soliton formation is a question of
further studies.
Generally about 40 soliton simulation experiments were conducted with
MVS-1000M. Six computational experiments of this array are presented in
this paper. The physical parameters were identical in all experiments,
but the number of particles and grid size were different. From the table
1 it follows that such experiments require large computatational resources.
To compute dust and gas motion even with a small grid it is necessary
to employ 8 processors. The computational experiments on finer grids were
conducted with the so called "checkpoints". A checkpoint means
that all the data of the program are saved to a file, one file for each
processor, and then the program stops. After a while, the computational
experiment is continued starting from the saved data.
| Grid size | Number of particles | Size of region under study | Center of region under study | |
| I | 120*128*128 | 10 million | 2.0*2.0 | (0.0, 0.0) |
| II | 200*256*128 | 25 million | 2.0*2.0 | (0.0, 0.0) |
| III | 200*256*128 | 25 million | 0.3*0.3 | (0.6, 0.6) |
| IV | 200*256*128 | 25 million | 0.4*0.4 | (-0.71, 0.1) |
| V | 300*256*128 | 50 million | 3.0*3.0 | (0.0, 0.0) |
| VI | 300*256*128 | 50 million | 1.0*1.0 | (0.5, 0.5) |
|
Table 3.Computational
experiments presented in the paper. |
||||
The difference between the computational experiments
is shown in the table 3. The computations are conducted with the grid
in cylindrical coordinate system. Nevertheless, to draw a 2D spatial
distribution of some function h(r,![]() )
a Cartesian grid is employed. This Cartesian grid is introduced in the
same domain and the distribution - now h(x,y) is computed on
this grid directly with particles.
)
a Cartesian grid is employed. This Cartesian grid is introduced in the
same domain and the distribution - now h(x,y) is computed on
this grid directly with particles.
Moreover, a small region of the disc is selected for detailed study,
and in this region the distribution h(x,y) is drawn with a
Cartesian grid of the same size as in the whole disc. The same way a
telescope shows some part of the sky in more detail. In the computational
experiments with the same grid size and the same number of particles
different regions of the disc where considered. From both the physical
and the computational point of view it is the same experiment. Nevertheless,
it is necessary to conduct a number of experiments with the same parameters
due to the following reasons. First, it is impossible to draw the distribution
in the whole disc in great detail. Second, it becomes clear which region
of the disc is worth studying in detail only when the experiment is
over. It should be noticed that there is no loss of precision, since
the distribution in a small part of the disc is also computed with particles.
The pictures in the section Soliton Structure are an exclusion
from this rule. They present distributions from the vicinity of the
soliton, that is, in a region of a very small size (less than 0.2 *
0.2). They are obtained by cutting the corresponding part of the grid
from the distribution in a large region.
Both in the whole disc and in small size regions the distribution is
drawn by the same rules: white color corresponds to maximal value, black
to zero, the scale is logarithmic.
Grid influence on the computational experiments.
Computational experiments with the same physical parameters were conducted
on the following sequence of grids: 120*128*128 nodes, 200*256*128 nodes,
300*256*128 nodes. The resulting distributions of particle density are
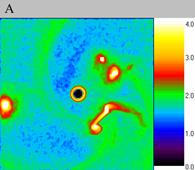
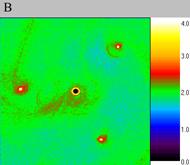
shown in fig. 1
 |
 |
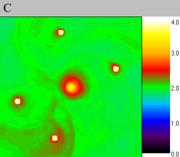 |
Fig. 1. Density
waves on different grids.
|
||
The size of the exposed domain is 2.0*2.0, coordinates
of the centre are (0.0, 0.0), moment of time is 4.0. A – 120*128*128
nodes (computational experiment I), B - 200*256*128 nodes (computational
experiment II), C - 300*256*128 nodes(computational experiment V).
Density waves that arise on the coarse grid (120?128?128 nodes) are
different from solitons in that they have large size, as it is seen
in fig. 1. A in comparison with figures 1B and 1C. Another difference
is that they are unstable. These density waves decay in a short period
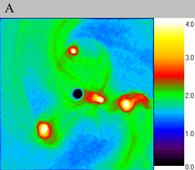
of time "delta" T = 0.4, fig. 2C
 |
 |
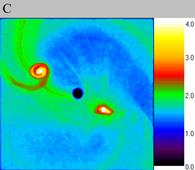 |
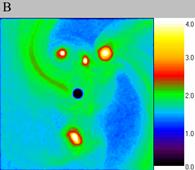
| Fig. 2. Decay of density waves on the coarse grid, computational experiment I. The size of the exposed domain is 2.0*2.0, the centre of it is in (0.0, 0.0). Figure A shows particle density distribution for the moment of time 4.4, figure B for the moment of time 4.8 and figure C for 5.2. | ||
On the contrary, on finer grids density waves have small size (fig. 3) and they remain stable during a large period of time, ?T = 4.0, figure 3, A, B and C. In fig. 3C it is seen that upper and lower solitons are shifted from initial position. But the most important result is that these density waves remain stable and keep small size.
 |
 |
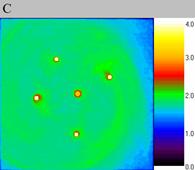 |
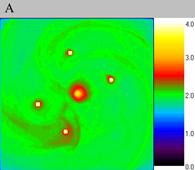
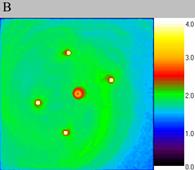
| Fig. 3.The stability of density waves on the fine grid, computational experiment V. The size of the exposed domain is 3.0*3.0, the centre of it is in (0.0, 0.0). Figure A shows particle density distribution for the moment of time 4.0, figure B for the moment of time 6.0 and figure C for 8.0. | ||
Soliton behavior:
Soliton is a lone density wave. On the fine grid (computational experiment
V) the solitons were nearly immobile during a short period of time. Considered
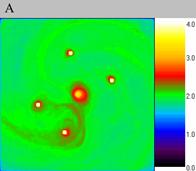
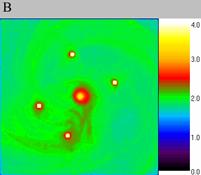
particle density distribution in dynamics it is clearly seen. In fig.
4 this distribution is shown in the three successive moments of time.
The difference in time between them is 0.2. The four solitons do not shift
during this short period, though the density distribution in the whole
disc changes significantly.
 |
 |
 |
| Fig. 4.The immobile solitons on the fine grid, computational experiment V. The size of the exposed domain is 3.0?3.0, the centre of it is in (0.0, 0.0). Figure A shows particle density distribution for the moment of time 4.0, figure B for the moment of time 4.2 and figure C for 4.4. | ||
The following fact proves that these structures are density waves and
not clumps of dust. The matter of the disc rotates around the disc centre,
but the solitons remain in its position. It should be noticed that in
fact the soliton moves as a density wave, but its velocity could be oriented
either along the flow or in the opposite direction.
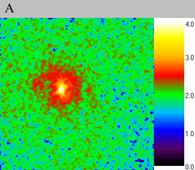
So the soliton form a small region of high density in the flow. It is
similar to a magnetic lens that focuses a beam of charged particles. The
difference is that the focusing field in the case of soliton is created
by the beam itself.
 |
 |
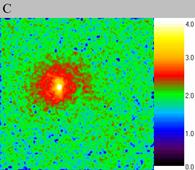 |
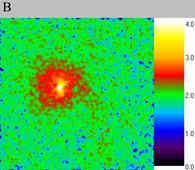
| Fig. 5.The immobile soliton scaled-up, computational experiment III. The size of the exposed domain is 0.3*0.3, the centre of it is in (0.6, 0.6). Figure A shows particle density distribution for the moment of time 4.01, figure B for the moment of time 4.05 and figure C for 4.09. | ||
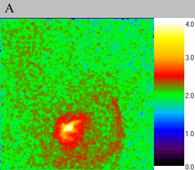
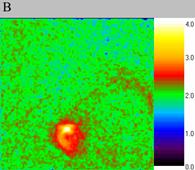
Let us consider the soliton scaled-up. With the same physical parameters the soliton either remained nearly immobile (computational experiment III, fig. 5) or oscillated around some point (computational experiment IV, fig. 6). Let us remind that these are two different solitons from the same computational experiment.
 |
 |
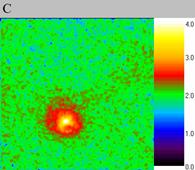 |
| Fig. 6.. The oscillating soliton scaled-up, computational experiment IV. The size of the exposed domain is 0.4?0.4, the centre of it is in (-0.71, 0.1). Figure A shows particle density distribution for the moment of time 4.01, figure B for the moment of time 4.09 and figure C for 4.17. | ||
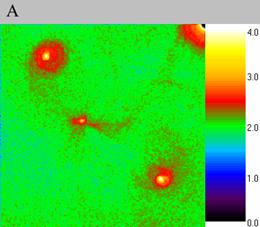
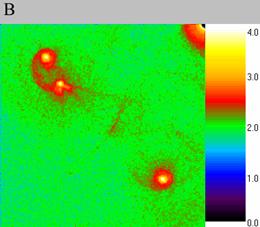
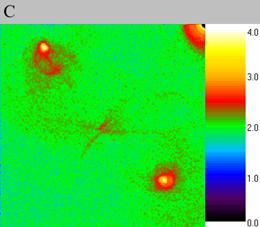
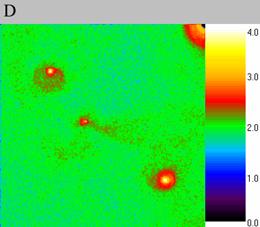
In the computational experiment VI the absorption of a density wave by soliton occured, fig. 7. First the density wave arises (fig. 7A), then it approaches the soliton (fig. 7B). After absorption the soliton deviates from the initial position (fig. 7C) but then returns back (fig. 7D). It should be noticed that such a phenomenon is impossible for clumps. Thus figure 7 proves wave nature of the structures observed in our computational experiments - the solitons.
 |
 |
|
|
T = 4.76 |
T = 4.96 |
|
 |
 |
|
|
T = 5.04 |
T = 5.2 | |
| Fig. 7..Absorption of a density wave by the soliton, computational experiment VI. The size of the exposed domain is 1.0*1.0, the centre of it is in (-0.5, -0.5). Figure A shows particle density distribution for the moment of time 4.76, figure B for the moment of time 4.96, figure C for 5.04 and figure D for 5.2. | ||
Literature:
1. Snytnikov V.N., Dudnikova G.I., Gleaves J.T., Nikitin S.A., Parmon
V.N., Stoyanovsky V.O., Vshivkov V.A., Yablonsky G.S.,Zakharenko V.S..
Space chemical reactor of protoplanetary disk. // Adv. Space Res. Vol.
30, No. 6, pp. 1461-1467, 2002
2. Yu.N.Grigoryev, V.A.Vshivkov, M.P.Fedoruk. Numerical “Particle-in-Cell”
Methods. Theory and Applications. VSP, 2002.
3. О.М.Белоцерковский, Ю.М.Давыдов. Метод крупных частиц в газовой динамике.
М: Наука, 1982.
4. A.V.Snytnikov. A Parallel Program for Simulation of Disc-Shaped Self-Gravitating
Systems. Bull.Nov.Comp.Center, Comp.Science. pp.73-81б V.19, 2003.
5. Снытников В.Н., Вшивков В.А., Дудникова Г.И., Никитин С.А., Пармон
В.Н., Снытников А.В. "Численное моделирование гравитационных систем
многих тел с газом". Вычислительные технологии номер 3, том 7. 2002,
с.72-84
6. E.A.Kuksheva, V.E.Malyshkin, S.A.Nikitin, A.V.Snytnikov, V.N.Snytnikov,
V.A.Vshivkov. Numerical Simulation of Self-Organisation in Gravitationally
Unstable Media on Supercomputers. PaCT-2003, LNCS 2763, pp.354-368, 2003.