
Assembly Technology Project
| Kraeva M.A., Malyshkin V.E. Assembly Technology for Parallel Realization of Numerical Models on MIMD-Multicomputers. In the special issue of the International Journal on Future Generation Computer Systems,devoted to Parallel Computing Technologies. Vol. 17 (2001), No. 6, pp. 755-765 |
1. Introduction
Parallel implementation of realistic numerical models, using direct modeling
of a physical phenomenon on the basis of description of the phenomenon
behaviour in the local area, usually requires high performance computations.
However these models are also remarkable for irregularity and even dynamically
changing irregularity of the data structure (adaptive mesh, variable time
step, particles, etc.). For example, in the PIC method the test particles
are in the bottom of such an irregularity. Additionally, parallel programs,
implemented realistic numerical models, should possess by new dynamic
properties like dynamic load balancing. Hence, these models are very difficult
for effective parallelization and high performance implementation with
conventional programming systems.
The Assembly Technology (AT) [1-3] has been especially created in order
to support the development of fragmented parallel programs for multicomputers.
Fragmentation and automatic dynamic load balancing are the key features
of programming and program execution under the AT. In order to provide
high performance of target programs the AT is implemented in different
ways for different application areas. In this paper, the application of
the AT to implementation of big size numerical models is demonstrated
on the example of parallel implementation of the PIC method [4,5].
2. The PIC method and the problems of its parallel implementation
The particle simulation is a powerful tool for modeling of the behaviour
of complex non-linear phenomena in plasmas and fluids. In the PIC method,
trajectories of a huge number of test particles are calculated as these
particles are moved under the influence of the electromagnetic fields
computed self-consistently on a discrete mesh. These trajectories represent
a desirable solution of the system of differential equations describing
a physical phenomenon under study.
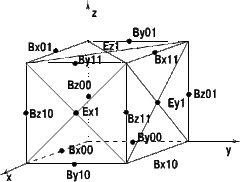
A real physical space is represented by a model of simulation domain called
the space of modeling (SM). The electric E and magnetic B fields are defined
as vectors and discretised upon rectangular mesh (or several shifted meshes,
as shown in Figs.1 and 2). Thus, as distinct from other numerical methods
on the rectangular mesh, in the PIC method there are two different data
structures – particles and meshes. None of the particles affects
another particle. At any moment of modeling a particle belongs to a certain
cell of each mesh.
Each charged particle is characterized by its mass, co-ordinates and velocities.
Instead of solution of equations in the 6D space of co-ordinates and velocities,
the dynamics of the system is determined by integrating the equations
of motion of every particle in the series of discrete time steps. At each
time step tk+1:=tk+Δt the following is done:
- for each particle, the Lorentz force is calculated from the values of electromagnetic fields at the nearest mesh points (gathering phase);
- for each particle the new co-ordinates and velocity of a particle are calculated; a particle can move from one cell to another (moving phase);
- for each particle the charge carried by a particle to the new cell vertices is calculated to obtain the current charge and density, which are also discretised upon the rectangular mesh (scattering phase);
- Maxwell's equations are solved to update the electromagnetic field (mesh phase).
 |
 |
| Fig. 1. A cell of the SM with the electric E and magnetic B fields, discretised upon shifted meshes | Fig. 2. The whole space of modeling (SM) assembled out of cells |
The sizes of a time step and of a cell are chosen in such a manner that a particle cannot fly farther than into the adjacent cell at one time step of modeling. The number of time steps depends on a physical experiment. The PIC algorithm has the great possibility for the parallelisation, because all the particles are moved independently. The volume of computations at the first three phases of each time step is proportional to the number of particles. About 90% of multicomputer resources are spent for the particle processing. Thus, in order to implement the PIC code on multicomputer with high performance, the equal number of particles should be assigned for processing to each processor element (PE). However, on the MIMD distributed memory multicomputers, the performance characteristics of the PIC code crucially depends on how the mesh and particles are distributed among the PEs. In order to decrease the communication overheads at the first and the third phases of a time step, it is required that a PE contains as the cells (values of the electromagnetic fields at the mesh points) as the particles located inside them. Unfortunately, in the course of modeling, some particles might fly from one cell to another. To satisfy the previous requirement, two basic decompositions can be used [4,5]. In the so-called Lagrangian decomposition, the equal number of particles are assigned to each PE with no regard for their position in the SM. In this case, the values of the electromagnetic fields, the current charge and density at all the mesh points should be copied in every PE. Otherwise, the communication overheads at the first and the third phases will decrease the effectiveness of parallelisation. Disadvantages of the Lagrangian decomposition are the following:
- strict memory requirements;
- communication overheads at the second phase (to update the current charge and the current density in each PE).
In the Eulerian decomposition, each PE contains a fixed rectangular sub-domain,
including electromagnetic fields at the corresponding mesh points and
particles in the corresponding cells. If a particle leaves its sub-domain
and flies to another sub-domain in the course of modeling, then this particle
should be transferred to the PE containing this latter sub-domain. Thus,
even with an equal initial workload of the PEs, in several steps of modeling,
some PEs might contain more particles than the others. This results in
the load imbalance. The character of the particles motion does not fully
depend on equations, but also on the initial particles distribution and
the initial value of the electromagnetic field.
Let us consider some examples of particles distribution, which correspond
to the different real physical experiments.
- Uniform distribution of the particles in the entire space of modeling.
- The case of a plate. The space of modeling has n1 x n2 x n3 size. The particles are uniformly distributed in k x n2 x n3 size space (k<<n1).
- Flow. The set of particles is divided into two subsets: the particles with zero initial velocity and the active particles with the initially nonzero velocity. Active particles are organized as a flow crossing the space along a certain direction.
- Explosion. There are two subsets of particles. The background particles with zero initial velocities are uniformly distributed in the entire space of modeling. All the active particles form a symmetric cloud (r<<h, where r is the radius of the cloud, h is the mesh step). The velocities of active particles are directed along the radius of the cloud.
The main problem of programming is that the data distribution among the
PEs depends not only on the volume of data, but also on the data properties
(particles velocities, configuration of electromagnetic field, etc.).
With the same volume of data but different particles distributions inside
the space the data processing is organized in different ways.
As the particles distribution is not stable in the course of modeling,
the program control and data distribution among the PEs should be dynamically
changing. It is clear that the parallel implementation of the PIC method
on a distributed memory multicomputer strongly demands the dynamic load
balancing.
3. Substantial features of AT
Numerical methods, generally, and the PIC method, in particular, are very suitable for the application of AT. The fragmented representation of an algorithm affects different stages of an application program development. Here we would like in brief to list some peculiarities of the AT.
3.1 Algorithm and program fragmentation
In accordance with the AT, the description of an application problem should
be divided into a system of reasonably small atomic fragments, representing
the implementation entities of a problem description. Fragments might
be represented in programming languages by variables, procedures, subroutines,
macros, nets, notions, functions, etc. depending on the method of the
AT implementation. The program, which realizes an atomic fragment (P_fragment),
contains both data and code. In other words, a program, realizing an application
problem, is assembled out of such small P_fragments of computations which
are connected through variables for data transfer.
The fragmented structure of an application parallel program is kept in
the executable code and provides the possibility for organization of flexible
and high performance execution of the assembled program. The general idea
is the following. An assembled program is represented in a programming
language, and is composed as a system of executable P_fragments. This
program is executed inside every PE, looping over all the P_fragments,
loaded to the PE. If these fragments are small enough, then initially
for each PE of a multicomputer the equal workload is assembled out of
these P_fragments. This is of course a general idea only. Actually, in
order to attain high performance of a target program its assembling is
realized in different ways.
The workload of PEs can be changed in the course of computation, and if
at least one PE becomes overloaded, then a part of P_fragments (with the
processing data), which were assigned for execution into the overloaded
PE, should fly to the underloaded PEs equalizing the workload of multicomputer
PEs. Dynamic load balancing of a multicomputer is based on such a fragmentation
[5,6]. The algorithms of a target program assembling out of atomic fragments
are not discussed here in detail.
3.2 Assembling vs. Partitioning
Our basic key word is assembly. Contrary to partitioning, the AT supports
explicit assembling of a whole program out of ready-made fragments of
computations, rather then dividing a problem, defined as a whole, into
the suitable fragments to be executed on the different PEs of a multicomputer.
These fragments are the elementary blocks, the "bricks", to
construct a whole program (a whole problem description), there is no a
difference here). An algorithm of a problem assembling is kept and used
later for dynamic program/problem parallelization. Assembling defines
the "seams" of a whole computation, the way of the fragments
connection. Therefore, these seams are the most suitable way to cut the
entire computation for parallel execution. For this reason program parallelization
can be always done if the appropriate size of atomic fragments is chosen.
3.3 Explicitly two-level programming
Under the AT, first, suitable atomic fragments of computation are designed,
programmed and debugged separately. Then the whole computation (problem
solution) is assembled out of these fragments.
3.4 Separation of the fine grain and the coarse grain computations.
The fine and the coarse grain computations are executed on the different
level of hardware and software. Under AT the fine grain computations are
encapsulated inside a module (P_fragment) that realizes the computations
bound up with atomic fragment. Such a module can be implemented very effectively
on a processor element. The whole parallel program is assembled out of
these ready-made modules. The system of modules of a program defines a
system of interacting processes (coarse grain computations). Encapsulation
of the fine grain computations, their complexity, inside an atomic fragment
provides the possibility of formalization of a parallel program construction
and the use of explicitly two-level representation of an algorithm: the
programming level inside an atomic fragment and the scheme level of an
application program assembling.
3.5 Separation of semantics and scheme of computation
The fine grain computations define a sufficient part of semantics (functions)
of computations. They are realized within an atomic fragment. Therefore,
on the coarse grain level, only a scheme (non-interpreted or semi-interpreted)
of computations is assembled. It means that formal methods of automatic
synthesis of parallel programs [1] can be successfully used and the standard
schemes of parallel computations can be accumulated in libraries.
4. Parallelization of numerical methods with AT
Let us consider the assembly approach to the numerical methods parallelisation
on the example of the PIC method parallel implementation.
The line and the 2D grid structure of interprocessor communications of
a multicomputer are sufficient for the effective parallel implementation
of numerical methods on the rectangular meshes. In [3] the algorithm of
the 2D grid mapping into the hypercube keeping the neibourhood of PEs
is given.
A cell is natural atomic fragment of computation for a numerical method
implementation. It contains both data (particles inside the cells of a
fragment and values of electromagnetic fields, current density at their
mesh points) and the procedures, which operate with these data. For the
PIC method, when a particle moves from one cell to another, it should
be removed from the former cell and added to the latter cell. Thus, we
can say that with the AT the Eulerian decomposition is realized.
4.1 PIC parallelization on the line of PEs
Let us consider first in what way the PIC is parallelized for the multicomputers
with the line structure of interprocessor communications. The three-dimensional
simulation domain is initially partitioned into N blocks (where N is the
number of PEs). Each block_i consists of several adjacent layers of cells
and contains approximately the same number of particles (Figs. 3, 4).
When the load imbalance is crucial, some layers of the block located into
an overloaded PE are transferred to another less loaded PE. In the course
of modeling, the adjacent blocks are located in the linked PEs. Therefore,
the adjacent layers are located in the same or in the linked PEs. It is
important for the second phase, at which some particles can fly from one
cell into another and for the fourth phase, when for recalculation of
values of electromagnetic fields in a certain cell, values in the adjacent
cells are also used.
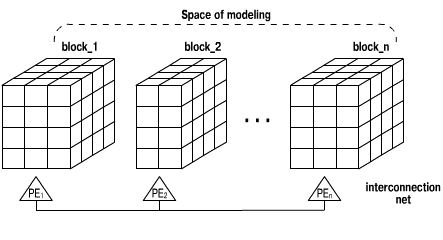 |
| Fig. 3. Decomposition of SM for implementation of the PIC on the line of PEs |
4.2 PIC parallelization on the 2D grid of PEs
Let us consider now the PIC method parallelization for the 2D grid of
PEs. Let the number of PEs be equal to lxm. Then SM is divided into l
blocks orthogonal to a certain axis. Each block consists of several adjacent
layers and contains about NP/l particles (in the same way as it was done
for the line of PEs). The block_i is assigned for processing to the i-th
row of the 2-D grid (Fig. 4). Blocks are formed in order to provide an
equal total workload of every PE's row of the processor grid. Then every
block_i is divided into m sub-blocks block_i_j, which are distributed
for processing among m PEs of the row. These sub-blocks are composed in
such a way in order to provide an equal workload of every PE of the row.
If overload of at least one PE occurs in the course of modeling, this
PE is able to recognize it at the moment when the number of particles
substantially exceeds NP/(lxm). Then this PE initiates the re-balancing
procedure.
 |
| Fig. 4. Decomposition of SM for implementation of PIC on the 2D grid of PEs |
If the number of layers k x N (or k x l in the case of the grid of PEs), it is difficult or even impossible to divide the SM into blocks with the equal number of particles. Also, if particles are concentrated inside a single cell, it is definitely impossible to divide SM into the equal sub-domains. In order to attain the better load balance, the following modified domain decomposition is used. A layer containing more than the average number of particles is copied at least into 2 or more neighbouring PEs (Fig. 5) – these are virtual layers. A set of particles located inside such a layer are distributed among all these PEs. In the course of the load balancing, particles inside the virtual layers are the first to be redistributed among PEs, and only if necessary, the layers are also redistributed. For the computations inside a PE, there is no difference between virtual and non-virtual layers. Any layer could become virtual in the course of modeling, a virtual layer can stop to be virtual.
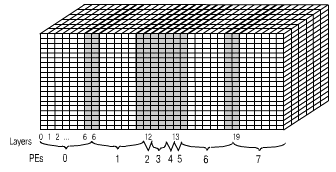 |
| Fig. 5. Virtual layers for implementation of PIC on the 2D grid of PEs |
We can see, that in both cases there is no a necessity to provide flying
of a cell. A cell is very small fragment, therefore a large resources
should be spent to provide its flying. Thus, there is a necessity to use
bigger indivisible fragments on the step of execution (not on the step
of a problem/program assembling!). In the case of the line of PEs a layer
of the SM should be chosen as indivisible fragment of concrete implementation
of PIC. Such a fragment is called a minimal fragment. For PIC implementation
on the grid of PEs a column is taken as minimal indivisible fragment.
Procedure realizing minimal fragment is composed statically out of P_fragments,
before the whole program assembling. This essentially improves the performance
of an executable code.
In such a way, a cell is used as atomic fragment at the step of numerical
algorithm description. At the step of execution of a numerical algorithm,
different minimal fragments assembled out of atomic fragments are chosen
depending on architecture of a multicomputer.
4.3 Implementation of the PIC method on multicomputers
Using AT PIC method has been implemented on different multicomputer systems
(MBC-100, multitransputer system, Hypercube Intel iPSC/860, Parsytec PowerXplorer,
Cray J90, IBM SP2). In order to provide a good portabilitym the language
C was chosen for the parallel PIC code implementation. Since different
message passing systems are used for different multicomputers, the special
communication functions were designed. In the compilation time the actual
functions of a target multicomputer are substituted instead of these communication
functions. In particular, the MPI functions might be substituted. For
the dynamic load balancing of PIC several algorithms were developed [7,8].
In the cases of the grid communication structure (Fig. 6) and the virtual
fragments (particles might fly not only to the neighbouring PEs) special
tracing functions are used.
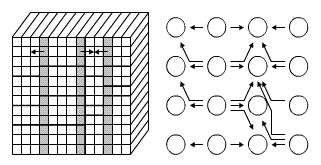 |
| Fig. 6. Direction of data transfer for implementation of the PIC on the 2D grid |
According to the AT the array of particles is divided into N parts, where N is the number of minimal fragments (layers of SM in the case of the line of PEs, and columns in the case of the 2D grid). When elements of the mesh variables (electromagnetic fields, current charge and density) of different minimal fragments hit upon the same point of SM, they are unified (Fig. 7). The elements of the mesh variables of one minimal fragment are not added to the data structure for this fragment, but are stored in the 3D arrays with elements of the mesh variables of other minimal fragments in the PE. This appears possible due to the rectangular shape of blocks block_i (block_i_j in the case of the 2D grid). Such a decision allows us to decrease the memory requirements and to speed up computations during the forth phase of the PIC algorithm.
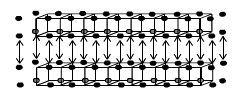 |
| Fig. 7. Unification of the Hx mesh variables for two minimal fragments (layers) |
In the case of dynamic load balancing, when some minimal fragments are transferred from one PE to another, the size of the 3D arrays of elements of the mesh variables is dynamically changed. This demands special implementation of such dynamic arrays.
5. Dynamic load balancing
To attain a high performance of parallel PIC implementation, a number of centralized and decentralized load balancing algorithms were especially developed.
5.1 Initial load balancing
A layer of cells is chosen as minimal fragment for the PIC implementation
on the line of PEs. Each minimal fragment has its own weight. The weight
of a minimal fragment is equal to the number of particles in this fragment.
The sum of weights of all the minimal fragments in some PE determines
the workload of PE. The 3D simulation domain is initially partitioned
with a certain algorithm into N blocks (where N is the number of PEs).
Each block consists of several adjacent minimal fragments and contains
approximately the average number of particles. For the initial load balancing
two heuristic centralized algorithms were designed [7,8]. These algorithms
employ the information about the weights of all the minimal fragments.
Each PE has this information and constructs the workload card by the same
algorithm. The workload card contains the list of minimal fragments that
should be loaded to the PEs. If the number of minimal fragments is much
greater than the number of PEs, it is usually possible to distribute the
minimal fragments among the PEs in such a way that every block would contain
approximately the same number of particles.
If considerable portion of particles is concentrated inside a single cell,
it is impossible to divide the SM into the blocks with quite an equal
workload. To solve this problem, a notion of virtual layer is introduced.
The centralized algorithm was modified for the case of virtual fragments.
If overloading of at least one PE occurs in the course of modeling, this
PE is able to recognize it at the moment when the number of particles
substantially exceeds NP/N. Then this PE initiates the re-balancing procedure.
5.2 Dynamic load balancing
If a load imbalance occurs, the procedure BALANCE is called. In this procedure,
the decision about the direction of data transfer and the volume of data
to be transferred is taken. For any load balancing algorithm there exists
its own realizing procedure BALANCE. The procedure TRANSFER is used for
the data transfer. There are two implementations of this procedure: for
the line of PEs and for the grid of PEs. The procedure TRANSFER is the
same for any load-balancing algorithm on the line of PEs. Parameters of
the procedure are the number of particles to be exchanged and the direction
of data transfer.
Let us consider algorithms of the dynamic load balancing of the PIC. All
the PEs are numerated. In the case of the line of PE, each PE has number
i, where 0<= i < number_of_PEs. In the case of the (l x m) grid
of PEs, the number of PE is the pair (i,j) , where 0 <=i < l, 0
<=j < m. In the same way, layers and columns of the SM are numerated.
5.3 Centralized dynamic load balancing algorithm
For the dynamic load balancing the initial load balancing algorithm could
be used. One of PEs collects the information about weights of the minimal
fragments and broadcasts this information to all the other PEs. All the
PEs build the new load card. After that neighbouring PEs exchange minimal
fragments according to the information in the new workload card.
Imbalance Threshold. If centralized algorithms are used for the dynamic
load balancing, the PEs exchange the information about load balancing,
therefore every PE has information about the number of particles in all
the PEs. In any PE, the difference mnp-NP/N (where mnp is the maximum
number of particles in PE, NP is the total number of particles, N is the
number of PEs) is calculated. If the difference is more than the threshold
Th, the procedure BALANCE is called. The threshold can be a constant,
chosen in advance, or an adaptive number. In the latter case, initially
Th=0. In the course of modeling, the time t_part, which is required to
implement steps 1)-3) of the PIC algorithm for one particle, is calculated.
After every BALANCE call the time of balancing t_bal is calculated. Th
is assigned to be equal to t_bal/t_part (how many particles could be processed
for the same time as one balancing requires). After each subsequent step
of the PIC algorithm, Th is decreased by mnp-NP/N. When the value of Th
is negative, BALANCE is called.
If the threshold is always equal to zero, the procedure BALANCE is called
after each time step of modeling.
5.4 Decentralized dynamic load balancing algorithm for the constant
number of particles
The use of centralized algorithms is good enough for multicomputers containing
a few PEs. But if the number of PEs is big enough, the communication overheads
could neutralize the advantages of the dynamic load balancing. In this
case it is more preferable to use decentralized algorithms. Such algorithms
use information about the load balance in the local domain of PEs only.
If the number of model particles is not changed in the course of modeling,
a simple decentralized algorithm could be suggested. Each PE has the information
on how many particles were moved to/from its neighbouring PEs. To equalize
the load balance it is sufficient just to receive/send the same number
of particles from/to the neighbouring PEs. It should be noted that this
algorithm works in the case of virtual fragments only.
5.5 Specialized decentralized algorithm
To equalize the load balance for the PIC implementation, the following
specialized algorithm was designed. In the course of modeling in every
PE the main direction of particles motion is calculated from the values
of particles velocities. In the load balancing, particles are delivered
to the direction opposite to the main direction. As in the previous algorithm
it is assumed that the number of particles is not changed in the course
of modeling. The number of particles to be transferred from overloaded
PEs to their neighbours in the direction opposite to the main direction
is calculated from the average number of particles and the number of particles
in the PE. Some particles are transferred in advance, in order to reduce
the number of calls of the dynamic load balancing procedure.
5.6 Diffusive load balancing algorithms
The basic diffusive load-balancing algorithm was implemented and tested
for the PIC parallel implementation [7-9]. The size of the local domain
is equal to two. Any diffusive algorithm is characterized by the number
of steps. Actually the number of steps defines how far the data from one
PE could be transferred in the course of load balancing. For every step
the procedure TRANSFER is called. The more the number of steps of diffusive
algorithm the better load balance could be attained, but also the more
time is required for load balancing. The tests have shown that the total
program time does not decrease with the growth of the number of steps.
5.7 Algorithms comparison
In the following Tables the results of different dynamic load balancing
algorithms testing for the problem of plasma cloud explosion modeling
are shown. The size of the problem is the following:
• The size of the space of modeling - 24x24x36
• The number of background particles - 24*24*36*27=559872
• The number of cloud particles - 240128
• The total number of particles - 800
| 2 PE | 3 PE | 4 PE | 5 PE | 6 PE | 7PE | 8 PE | 20 PE | |
| The max number of particles in PE | 400000 | 353256 | 223190 | 207663 | 213364 | 153948 | 152389 | 79930 |
| Duration of particles processing | 110190 | 97462 | 62012 | 57375 | 59072 | 42821 | 46980 | 22267 |
| Total time | 121768 | 107878 | 68801 | 63481 | 65332 | 47470 | 46716 | 24687 |
Tab.1
Dynamic load balancing is absent |
||||||||
| 2 PE | 3 PE | 4 PE | 5 PE | 7 PE | 8 PE | |
| The max number of particles in PE | 400000 | 266787 | 200102 | 160091 | 114388 | 100091 |
| Duration of particles processing | 110625 | 73862 | 55722 | 44498 | 32189 | 27579 |
| Total time | 122294 | 81900 | 61902 | 49453 | 35826 | 30744 |
Tab.2
Centralized load balancing algorithm |
||||||
| 2 PE | 3 PE | 4 PE | 5 PE | 6 PE | 7PE | 8 PE | 20 PE | |
| The max number of particles in PE | 400000 | 266977 | 200001 | 160484 | 133679 | 153948 | 100727 | 42092 |
| Duration of particles processing | 110459 | 75116 | 56246 | 45036 | 59072 | 37270 | 28260 | 11887 |
| Total time | 122048 | 83191 | 62606 | 50083 | 65332 | 47470 | 31508 | 13353 |
Tab.3
Diffusive load balancing algorithm (the number of steps is equal
to 2) |
||||||||
| 2 PE | 3 PE | 4 PE | 5 PE | 6 PE | 7 PE | 8 PE | 20 PE | |
| The max number of particles in PE | 400000 | 328325 | 200000 | 161630 | 133473 | 115489 | 100238 | 41388 |
| Duration of particles processing | 110329 | 90333 | 56203 | 45926 | 36821 | 32669 | 28504 | 11647 |
| Total time | 121952 | 100022 | 62337 | 50946 | 40980 | 36419 | 31801 | 13093 |
Tab. 4 Specialized
decentralized algorithm |
||||||||
If the number of PEs is greater than 2, the load balancing is required. The results of the tests confirm the fact, that for the small number of PEs (less than 10), the utilization of a centralized algorithm is more preferable, though decentralized algorithms also give satisfactory results.
6. Automatic generation of parallel code
The PIC method is applied to simulation of many natural phenomena. In
order to facilitate the parallel PIC implementation, a special system
of parallel program automatic generation was designed. This system consists
of the VISual system of parallel program Assembling (VisA) and a parallel
code generator in C language.
The process of the generation of a parallel program for the PIC and for
the other numerical algorithms on the rectangular meshes consists of three
steps.
At the first step, a user defines the atomic fragment of computation –
a cell of the SM. This cell contains elements of the mesh variables at
several mesh points, an array of particles (for PIC method) and procedures
in C language, which describe all the computations inside the cell – {procedure1,…,procedurek}
(Fig. 8).
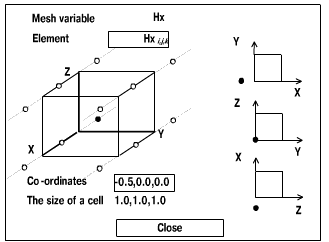 |
| Fig. 8. Review window for Hx mesh variable of an atomic fragment of computation |
On the next step the user chooses the target multicomputer and the topology
of the communication net, for which the parallel code should be generated.
After that the generator constructs a minimal fragment (a layer or a column)
from the atomic fragments according to the chosen communication topology.
The particle arrays of atomic fragments merge to a single particle array
for the minimal fragment. The elements of the mesh variables, which hit
upon the same point of SM, are unified. In such a way, for every mesh
variable, only one 3D array of its elements is formed.
At the third step, the decision on the PEs workload is made. The generator
creates a parallel program for a target multicomputer. This program includes
data initialization and a time loop. At each iteration of the time loop,
k loops (where k is the number of procedures in the description of an
atomic fragment) over all the minimal fragments of PE run. After each
k-th loop, those elements of the mesh variables, which are copied in several
PEs, are updated (if necessary).
All the particles are stored in m arrays (where m is the number of minimal
fragments in a certain PE). However, similarly the case of the minimal
fragment assembling, the elements of a mesh variable in all the minimal
fragments of a PE form one 3D array.
The user develops procedures (computations inside a cell) in C language,
using also several additional statements for defining the computations
over the mesh variables.
7. Conclusion
The described algorithms of the numerical models assembling provide high
performance of the assembled program execution, its high flexibility in
reconstruction of the code and dynamic tunability to available resources
of a multicomputer.
High performance of the program execution provides the modeling of big
size problems such as the study of a cloud plasma explosion in the magnetized
background, modeling of interaction of a laser impulse with plasma, etc.
We apply the assembly technology to implementation of different numerical
methods and hope to create a general tool to support implementation of
mathematical approximating models.
Publications:
1. V.A.Valkovskii, V.E.Malyshkin. Synthesis of Parallel Programs and Systems
on the Basis of Computational Models.// Nauka, Novosibirsk, 1988. (In
Russian)
2. V.Malyshkin. Functionality in ASSY System and Language of Functional
Programming.// Proc. "The First Aizu International Symposium on Parallel
Algorithms/Architecture Synthesis", 1995, Aizu-Wakamatsu, Fukushima,
Japan. IEEE Comp. Soc. Press, Los Alamitos, California. P. 92-97.
3. Kraeva M.A., Malyshkin V.E. Assembly Technology for Parallel Realization
of Numerical Models on MIMD-Multicomputers. In the special issue of the
International Journal on Future Generation Computer Systems, devoted to
Parallel Computing Technologies. Vol. 17 (2001), No. 6, pp. 755-765.
4. M.Kraeva, V.Malyshkin. Implementation of PIC Method on MIMD Multicomputers
with Assembly Technology.// Proc. of HPCN Europe 1997 (High Performance
Computing and Networking) Int. Conference, LNCS, Vol.1255, Springer Verlag,
1997. pp. 541-549.
5. M.A.Kraeva, V.E.Malyshkin. Algorithms of Parallel Realization of PIC
Method with Assembly Technology. In Proceedings of 7th HPCN Europe 1999,
Springer Verlag, LNCS, Vol. 1593, pp.329-338.
6. M.Kraeva, V.Malyshkin. Dynamic load balancing algorithms for implementation
of PIC method on MIMD multicomputers.// Programmirovanie, 1999, N 1, p.47-53
(in Russian)
Supervisor: Malyshkin
V. E. (
)
Ph. D. Student: Nechaev
S. P. (
)